| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 백준 3085번
- 모각코
- MySQL
- 다이나믹 프로그래밍
- AWS
- java_programming
- 머신러닝과 딥러닝
- 자바
- 백준 16918번
- 알고리즘
- 그래프
- javascript
- Python
- 백준
- 백준 2512번
- 깃헙
- HUFS 모각코 캠프
- 그리디
- 백준 1987
- 백준 15787번
- SQL
- 백준 17451번
- react
- 백준 1331번
- 다이나믹프로그래밍
- 명품자바
- 백준 18310번
- SWEA 15612번
- ubuntu
- 백준 1253번
- Today
- Total
차곡차곡
Linear Algebra 본문
Systems of Linear Equations
실제 문제들은 linear equation 형태로 만들어질 수 있다. 그리고 linear algebra가 그 문제들을 푸는 데 툴을 제공한다.
*Linear Algebra : linear equation(Ax=b)로 표현 가능한 system을 푸는 방법론. 선형성(linearity)을 가지는 대수(algebra)로 이루어진 방정식의 해를 구하는 방법론
모든 문제는 해가 없거나(방정식 평행), 해가 1개(intersection 존재)이거나, 무수히 많은 해(하나의 방정식으로 표현 가능)가 존재한다.

Matrices
[Scalars]
크기만 있고 방향성은 없는 성분 (상수)
[vectors]
An array of numbers; arranged in order
벡터 공간의 원소
크기와 방향을 모두 갖고 있다.
[Matrices and Tensors]
1. Matrices : 2차원 array로 각각의 원소는 두 개의 첨자를 가진다.
ex) 높이 m, 너비 n, A ∈ R^(mxn)
┌ a₁,₁ a₁,₂ ┐
└ a₂,₁ a,₂,₂ ┘
2. Tensors : 3차원 이상의 array가 필요할 때
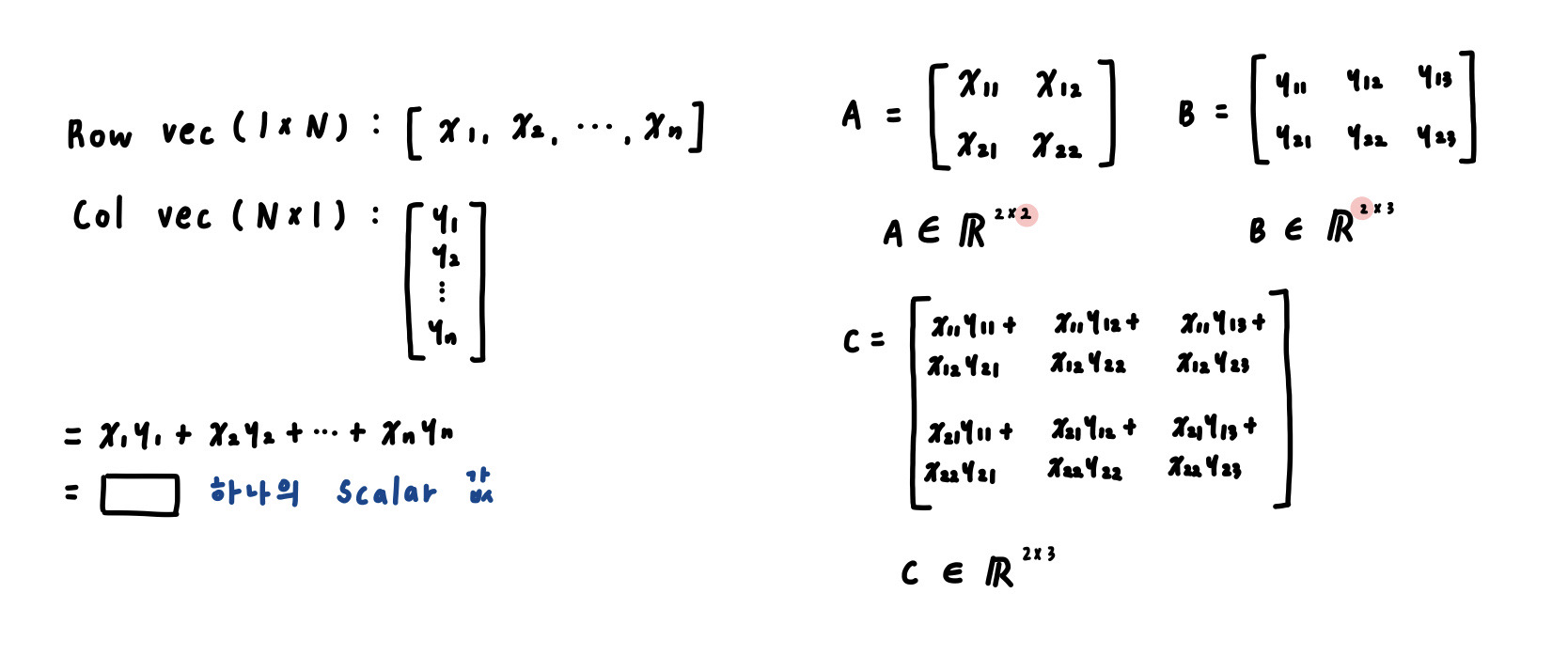
[Matrix Multiplication]
1. Matrix product
matrix A x matirx B = matrix C
*A의 행 개수와 B의 열 개수가 같아야 한다.
A ∈ R^mxn, B ∈ R^nxk >> C ∈ R^mxk

2. Hadamard product
같은 자리에 있는 원소끼리 곱
*matrix의 shape이 서로 같아야 한다.

[Identity Matrix]
어떠한 matrix에 곱해도 자기 자신이 나오게 하는 matrix. 주대각선의 원소가 모두 1이고 다른 원소는 모두 0이다.
AI = A
Im A (Im ∈ R^mxm) = A In (In ∈ R^nxn) = A (앞에서 곱하면 m차원, 뒤에서 곱하면 n차원)

[Inverse and Transpose]
1. Inverse (역행렬)
AA^-1 = I
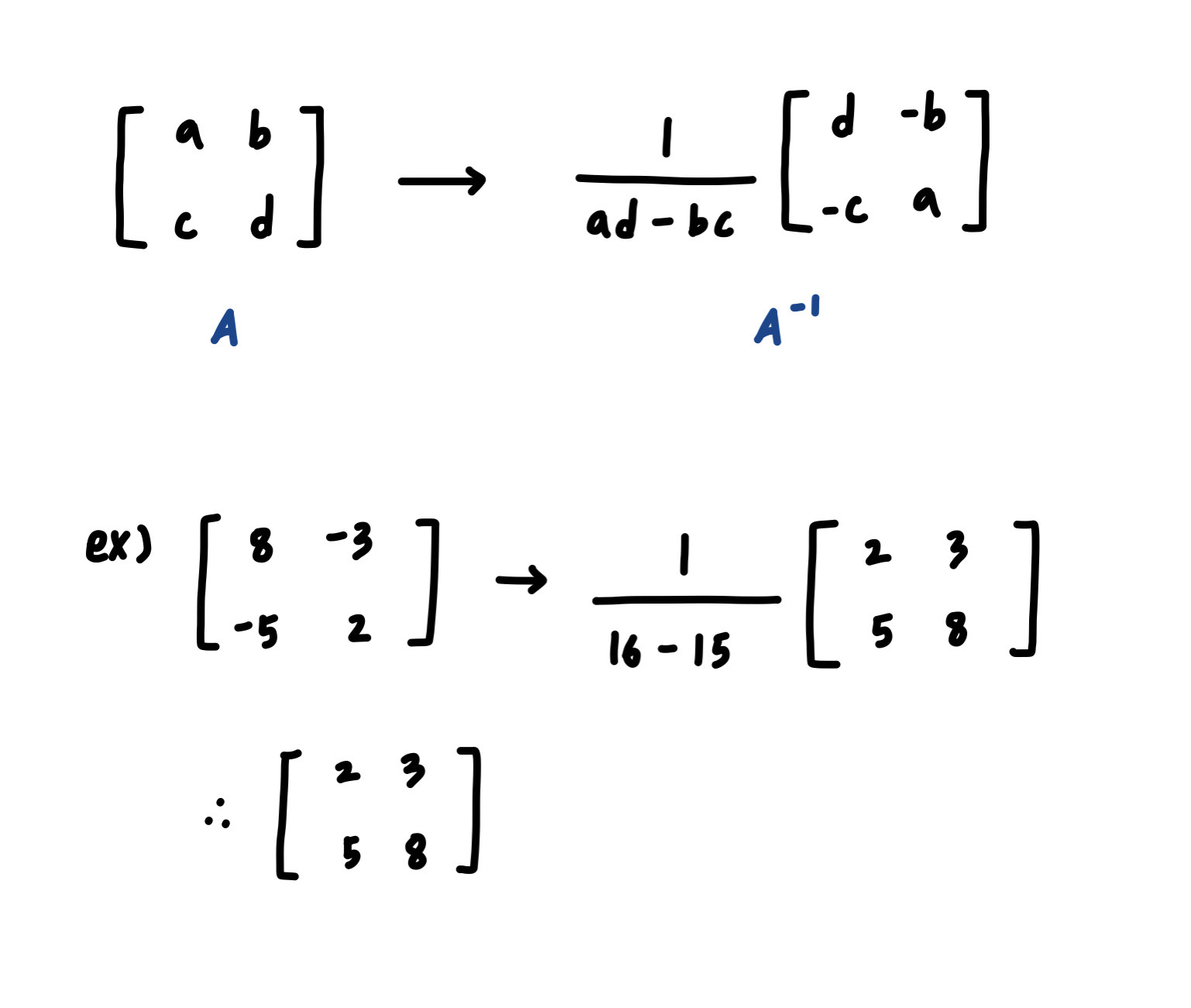
2. Transpose
행열을 바꾸는 것
A ∈ R^mxn >> A ∈ R^nxm, aij >> bji
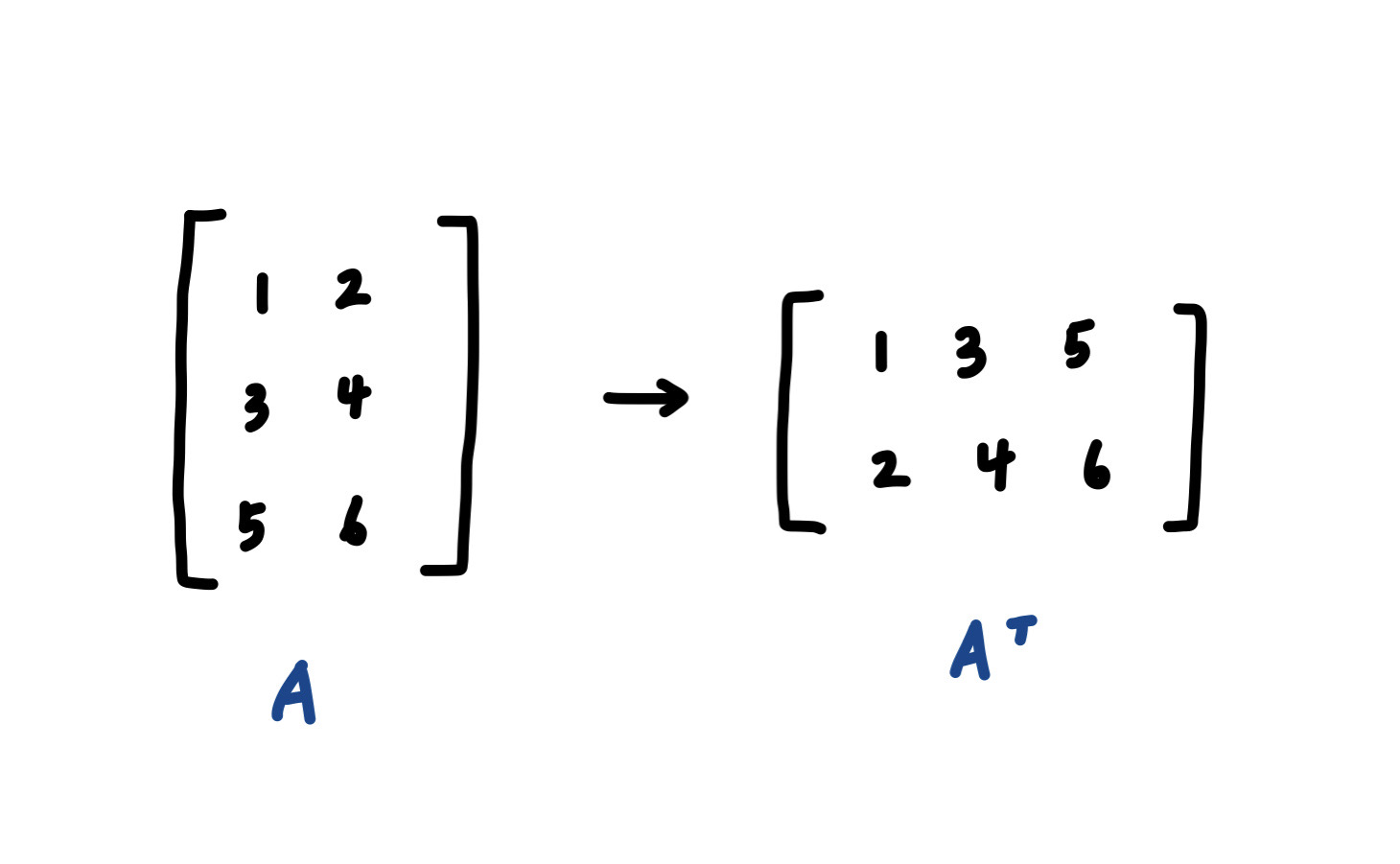
[Symmetric Matrix]
A가 A=A^T 이고, square matrix인 경우 A와 A^T는 symmetric 하다.
Solving Linear Systems
[Row Picture and Column Picture]
1. Row picture
각 row에 해당하는 방정식을 한 번에 하나씩 보는 것. equation을 좌표측에 표현해 교점을 찾아나가는 방식이다.
2. Column picture
행렬에서 column 방향으로 확인. 두 벡터를 이용해 최종 벡터에 도달하게 만드는 방식이다. (벡터는 방향과 크기가 같으면 같은 벡터)
* 1) 벡터에 음수가 가해지면 정반대 방향으로 이동한다. 2) 벡터가 항상 정수로 움직이는 것은 아니다.

[Elimination]
3개의 linear equations를 system matrix로 표현해 기준이 되는 식에 상수를 곱하고, 제고하고자 하는 식에서 소거하는 과정을 진행한다. 주대각선 아래 요소들을 0으로 만들어 upper triangular matrix를 만들어준다. (A matrix만 이용)

[Back Substitution]
A, B를 동시에 이용하는 augmented matrix를 형성하여 elimination을 진행한다. 3번째 row부터 해를 얻어 나간다.

(보라색 : pivot, 기준이 되는 칼럼. pivot을 제외한 나머지 요소들을 0으로 만들어줌)
# 문제를 푸는 방법으로서 geometric하게 row picture로 교점을 계산하는 것과, column picture로 벡터 개념을 통해 해에 도달하는 방법이 있다. 그리고 elimination을 이용한 back substitution을 통해 미지수를 구해나가는 방법이 있다.
[Gaussian Elimination]
2x2 matrix에 대한 inverse가 아닌 더 큰 차원에서의 inverse를 구하고 싶을 때 사용된다.
A 옆에 Identity Matrix를 붙인 후, A를 Identity Matrix로 만들어준다. 최종적으로 나온 Identity Matrix가 A의 inverse가 된다.
Vector Spaces
[vector spaces]
vector가 위치하는 공간. 미지수 vector가 해를 찾을 수 있는 공간이다. (즉, 해 공간)
vector space V = (v, +, .) 벡터 v와 두 개의 operation이 가능한 공간
vector space에 속해 있는 element x들을 vector라고 한다.
다루려는 데이터에 따라 vector space의 dimension이 달라진다.
*vector space에서 탐색을 하면서 실제와 가장 유사한 최적해를 찾아나가는 것이 머신러닝
[vector subspaces]
제약조건이 있을 경우, 넓은 공간의 해를 모두 사용할 수 있는 것이 아니라 일부로 한정된다. 이 경우 vector subspace가 존재한다. 즉, vector space의 일부에 해공간이 있는 것.
vector subspaces는 크게 4가지로 나뉜다.

Linear Independence
[Linear Combination]
하나와 infinitely many solutions 사이에 다수의 해가 존재할 수 없다. 위에 설명한 세 가지의 solution만이 존재할 수 있다.
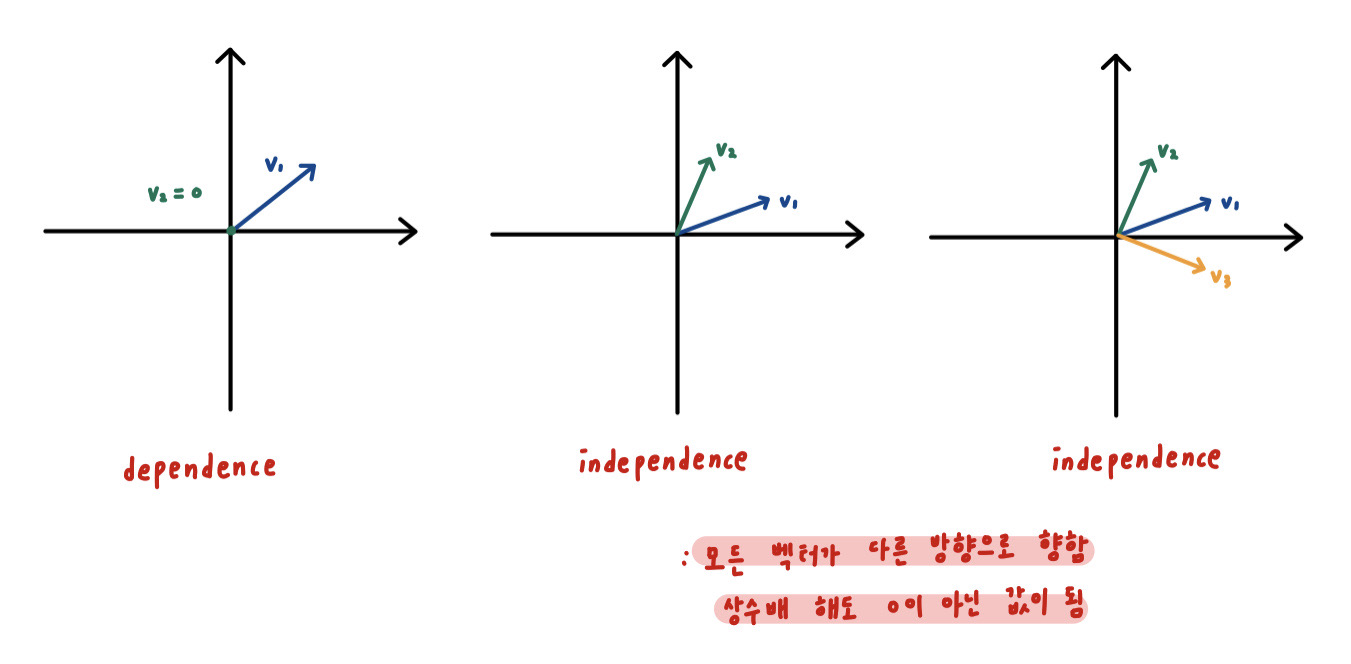
[Linear Independence]
(상수 벡터, 미지수 벡터 inner product)
두 vector가 independence : c1x1 + c2x2 + ... + cnxn ≠ 0, except for all ci=0
두 vector가 dependence : c1x1 + c2x2 + ... + cnxn = 0, for ci = any value
Basis and Rank
[Basis]
vector space에서 가장 기본이 되는 벡터. basis 벡터를 기준으로 해 공간 내 모든 벡터를 표현할 수 있다.
n차원의 vector space에서 dimension을 구성하고 있는 기저 벡터가 n개 존재한다. 해 공간의 모든 벡터는 n개의 기저 벡터를 linear combination 하여 만들어진 것이다. 그렇게 했을 때 값이 0이 나오면 안 되기 때문에 해 공간 내 모든 경우가 항상 independent 해야 한다.
the dimension of the vector space = the number of basis vectors

# system의 목적은 미지수 벡터를 찾는 것으로, 미지수 벡터는 vector space에 존재한다. 그리고 그 vector space를 구성하는 minimal한 벡터가 basis 벡터이다.
[Rank]
원래 있던 데이터를 나눠서 column차원의 공간에 뿌린 것. column차원으로 이루어진 vector space를 rank라고 한다.
정보와 정보 사이의 relationship을 고려해줄 수 있는 vector space이다.
rank는 matrix의 independent column 개수와 같다
